Rocket speed
How fast does a rocket have to travel to reach space?
 © GFDL
|
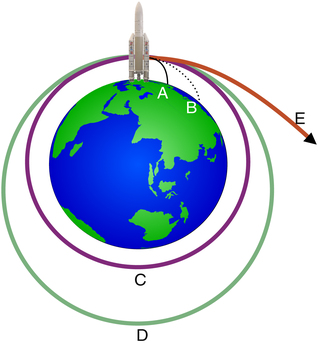
A rocket reaching the orbital velocity (1st cosmic velocity) will enter into orbit around the Earth (C), higher speed will lead to an elliptical trajectory (D). When the escape velocity (2nd cosmic velocity) is attained, the rocket will move away (E).
We could leave the Milky Way
At the start of the space age, Russian scientists applied the term 'cosmic velocities' to certain velocities that are important for space exploration. The 'first cosmic velocity', known as the orbital velocity, will bring a rocket or other projectile into orbit around the Earth. A slower projectile will fall back to Earth.The 'second cosmic velocity' is the so-called escape velocity from the Earth: 11.2 kilometers per second. This is the speed a rocket should attain in order to be able to escape from the Earth’s gravitational field and fly to other planets. It follows from the laws of orbital mechanics that the escape velocity (11.2 km/s) is equal to the orbital speed (7.9 km/s) multiplied by 1.414 (i.e. by the square root of 2).
If a spacecraft travels fast enough it is also possible to leave the Milky Way behind.
The 'third cosmic velocity' is the speed that a spacecraft needs to attain in order to be able to leave our solar system. This solar system escape velocity is about 42 kilometers per second (or 0.014 percent of the speed of light in a vacuum). Again, this is the product of the orbital velocity and the square root of 2. However, the orbital velocity now refers to the speed at which the Earth revolves around the Sun: about 30 kilometers per second multiplied by the square root of 2 equals about 42 kilometers per second. The ‘fourth cosmic velocity’ is the escape velocity from our galaxy - the Milky Way. It corresponds to about 320 kilometers per second.
It is important to bear in mind that these cosmic velocities are idealized values. For instance they do not take into account the loss of speed due to air resistance when a rocket is launched. Moreover, the values mentioned above are specific to the Earth and our solar system, and they do not apply to other parts of the universe.
Credit: German Aerospace Center
Rocket speed
How fast does a rocket have to travel to reach space?
 © GFDL
|
A rocket reaching the orbital velocity (1st cosmic velocity) will enter into orbit around the Earth (C), higher speed will lead to an elliptical trajectory (D). When the escape velocity (2nd cosmic velocity) is attained, the rocket will move away (E).
We could leave the Milky Way
At the start of the space age, Russian scientists applied the term 'cosmic velocities' to certain velocities that are important for space exploration. The 'first cosmic velocity', known as the orbital velocity, will bring a rocket or other projectile into orbit around the Earth. A slower projectile will fall back to Earth.The 'second cosmic velocity' is the so-called escape velocity from the Earth: 11.2 kilometers per second. This is the speed a rocket should attain in order to be able to escape from the Earth’s gravitational field and fly to other planets. It follows from the laws of orbital mechanics that the escape velocity (11.2 km/s) is equal to the orbital speed (7.9 km/s) multiplied by 1.414 (i.e. by the square root of 2).
If a spacecraft travels fast enough it is also possible to leave the Milky Way behind.
The 'third cosmic velocity' is the speed that a spacecraft needs to attain in order to be able to leave our solar system. This solar system escape velocity is about 42 kilometers per second (or 0.014 percent of the speed of light in a vacuum). Again, this is the product of the orbital velocity and the square root of 2. However, the orbital velocity now refers to the speed at which the Earth revolves around the Sun: about 30 kilometers per second multiplied by the square root of 2 equals about 42 kilometers per second. The ‘fourth cosmic velocity’ is the escape velocity from our galaxy - the Milky Way. It corresponds to about 320 kilometers per second.
It is important to bear in mind that these cosmic velocities are idealized values. For instance they do not take into account the loss of speed due to air resistance when a rocket is launched. Moreover, the values mentioned above are specific to the Earth and our solar system, and they do not apply to other parts of the universe.
Credit: German Aerospace Center